研究の動機

　川原の石の研究を始めたきっかけは、小学校1年生の時に家族で川へ遊びに行ったことだった。川原で石を投げて遊んだのだが、とてもたくさんの石があるのを見て、「この石たちは、どこからやってきたのだろう?」と不思議に思った。「きっと、海から波で運ばれたに違いない。調べてみよう！」と思いついたのが、始まりだった。
　５年生までの調査データを分析すると、安倍川の河口から20km地点で、上流よりも下流の石のほうが大きくなるという「逆転現象」が見られた。理科の授業で、上流の石が流水の働きで下流に運ばれるうちに削られて小さくなると学んだが、異なる調査データとなった。
　6年生の今回は、この「逆転現象」の原因について追究し、さらに天竜川でも逆転現象が起きていないかを調査した。これまでの調査データと、新たに行った調査をもとに分析、考察した。

研究の仮説

仮説1・安倍川の「逆転現象」は中河内川が原因

　これまで安倍川で調査してきた地点は、A～Gまで7か所ある。各地点の河口からの距離は、A地点が4km、B地点6km、C地点11km、D地点20km、E地点27km、F地点36km、G地点49kmだ。そのうち、D地点だけが唯一、上流の地点よりも石が大きくなっていた。河川事務所の調査でも20km地点の石が上流より大きいことが確認されているから、この「逆転現象」は測定ミスではなく、実際に起きている現象だといえる。
　D地点から2km上流（河口から22km）に、安倍川の支流である中河内川と、本流の安倍川との合流点がある。もし中河内川から安倍川へ、安倍川より大きな石が流れ込んでいるとしたらどうだろう。２km下流のD地点で、安倍川上流より大きな石が見つかる「逆転現象」が起きても不思議ではない。中河内川から安倍川へ大きな石が流れ込む可能性について、国土交通省中部地方整備局静岡河川事務所を訪問し、調査課の谷口淳先生に意見を聞いてみた。
　すると谷口先生は「残念ながら手元に中河内川の石のデータや資料はないが、中河内川からかなり大きな石が安倍川に供給されている可能性は高い」と答えてくれた。そこで、「逆転現象」は中河内川から流れ込む大きな石が原因で起こっているという仮説を立て、中河内川の石の大きさを調査することにした。

仮説2・天竜川では「逆転現象」は起こらない

　安倍川だけでなく、大井川と瀬戸川でもこれまで石の調査を行ってきたが、2つの河川で「逆転現象」は起こっていなかった。それでは、天竜川ではどうなのか。
　天竜川は静岡県で最も川の長さが長く（213km）、暴れ川として有名な1級河川である。川の斜面の傾き（河床勾配）は、大井川や安倍川と比べゆるやかだ。大きな支流も流れ込んでいないので、「逆転現象」は起こっていないという仮説を立て、確認のために調査した。

研究の方法

石の大きさの調査方法

　2つの仮説を立証するため、中河内川と天竜川の石の大きさを調査する必要がある。
　調査地点は、中河内川は安倍川との合流地点を起点とし、天竜川は河口を起点として決める。起点から数km〜数十kmの間隔で、A地点、B地点、C地点と順に調査地点を決めていく。川原へ安全に降りることができる道がない場合は、調査地点の間隔が何十kmと離れてしまうこともある。
　各調査地点では任意の場所に30cm四方の枠を置き、枠の中に入った石の中から大きい順に10個の石を選んだ。石の一部が入れば、枠に入った石とする。そして、選んだ石の一番長い部分の長さ（長径）を測定した。

　この10個の石の測定を1セットとして、各地点で2セットの調査をした。2セット目の調査は、1セット目の調査地点から5～10mほど離れた場所で行った。
　静岡河川事務所でも同じような調査をしているが、1m四方の100個の大きな石の測定を2セット行うそうだ。100個の石を測定したほうが、確かに正確なデータが得られるだろう。しかし、1年生の時から30cm四方の10個の石を測定してきたので、同条件の調査のほうが過去のデータや資料と比較しやすいと考えた。

研究の結果

中河内川の研究結果

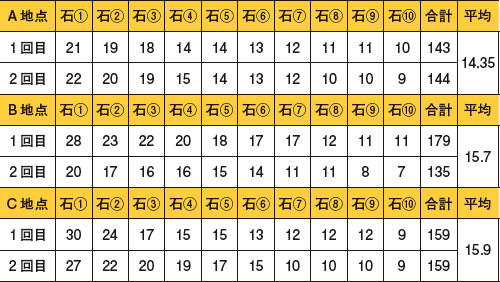
　中河内川では、A〜C地点の3地点で石の大きさを調査した。安倍川との合流地点がA地点、合流地点から4km上流のB地点、合流地点から7km上流のC地点だ。
　各地点で2セット測定した石の平均長径は、A地点が14.35cm、B地点が15.7cm、C地点が15.9cmだった。
　この結果から、中河内川では「逆転現象」は起こっていないことがわかった。

中河内川3地点での調査結果と石の大きさの平均（cm）

天竜川の研究結果

　天竜川では、A〜H地点の8か所でそれぞれ、石の大きさを調査した。河口からの距離は、A地点が3.5km、B地点が12km、C地点が18km、D地点が23km、E地点が30km、F地点が39km、G地点が48km、H地点が73kmだ。
　各地点で2セット測定した石の平均長径は、A地点が8.25cm、B地点が11.2cm、C地点平が11.75cm、D地点が12.45cm、E地点が23.7cm。F地点が14.75cm、G地点が19.5cm、H地点が15.1cmだった。
　天竜川では上流よりも石が大きい「逆転現象」が、E地点とG地点の2か所で起こっていた。

仮説1について

　安倍川で「逆転現象」が起こっていたのは、河口から20kmのD地点だ。D地点の石の平均長径は14.35cmで、より上流にあるE地点の平均長径12.55cmより大きい。しかし中河内川のB地点とC地点の平均長径はもっと大きく、15cmを超えている。「逆転現象」が起こった安倍川のD地点では、上流のE地点から流れてきた平均12〜13cmの石と、中河内川から流れてきた15cmを超える石が混じって、平均が14.35cmになったと考えられる。このことから、仮説1は正しい。

仮説2について

　今回の調査で天竜川でも「逆転現象」が起こっていることがわかったので、仮説2の予想は裏切られた。ただ、天竜川のE地点やG地点には支流の影響はない。地図をよく見てみると、E地点の上流には船明ダム、G地点の上流には秋葉ダムがあることがわかった。ダムの放水時の大きな力（掃流力）で本来は動かないような大きな石が下流へ転がり、放水の力が及ばなくなった地点で取り残された結果が、天竜川の「逆転現象」だと考えた。