研究の動機

　佐賀大学の講義「身のまわりの数学」で、２枚の透明な平行板を３本以上のピンでとめて、石けん液の中につけて引き上げると、ピンの間に張った石けん膜が全てのピンを結ぶ最短経路を示すということを知った。なぜ最短経路となるのか。自分で実験し、証明しようと思った。

〈１〉石けん膜の実験

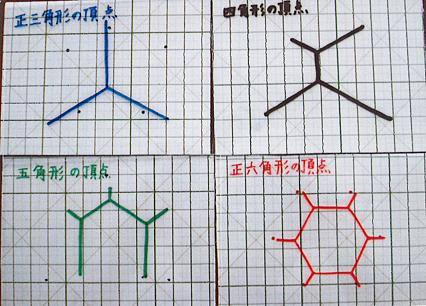
《方法》

２枚の透明なプラスチック板に３～７本の釘を、それぞれ三角形～七角形の頂点となるようにさして、間隔が２㎝くらいの平行板を作った。それを砂糖と洗剤を混ぜた石けん液の中につけて、引き上げた。

《結果》

三角形の場合、石けん膜は３頂点を結ぶ１点で交わった。３頂点への３本の線分は互いに120°の角度となった。この１点を「フェルマー点」と呼ぶという。四角形の場合、１回石けん液につけると、フェルマー点は２つできた。五角形の場合はフェルマー点は３つできた。六角形の場合、フェルマー点は１つできた。七角形の場合、フェルマー点は２つ、あるいは３つできた。

〈２〉 数学的な証明

　フェルマー点がなぜ120°で分けられるのか。数学的に問題を置き換え、３点（三角形）の場合で証明する。

問題：△ABCは∠A、∠B、∠C≦120°とする。△ABCの中に動点Pをとる時、AP＋BP＋CPを最小にするPの位置を求めよ。
（ⅰ）△ABCを正三角形とした時、PからAB、BC、CAへ垂線を下した点をそれぞれL、M、Nとし、PL、PM、PNをそれぞれx、y、zとする。

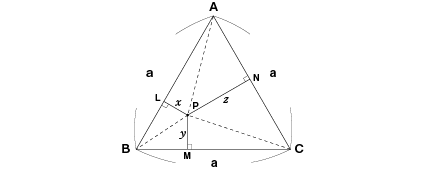図１

この△ABC の１辺の長さをaとする時の面積Sは、

一方、図１から、

ゆえに、

から

【定理】正三角形において、Pによらずx+y+zは一定である。

（ⅱ）実験から、Pの回りを120°ずつ分ける時、AP＋BP＋CPが最小になると分かった。ここで、それがなぜかを証明する。

　条件に合う任意の三角形の内部にAPo、BPo、CPoで120°ずつ分けるような点Poを置く。またA、B、Cの点でAPo、BPo、CPoから垂線を引いてできる三角形は正三角形である。ここで、その正三角形を△A´B´C´とし、△ABCの中に任意の点Pを置き、そのPからA´B´、B´C´、C´A´まで垂線を下した点をL、M、Nとする。

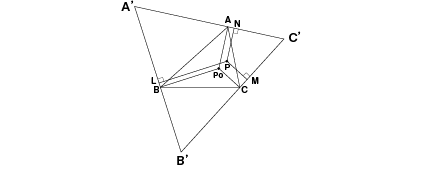図２

よってLP＋NP＋MPは、
（ⅰ）の定理により、APo＋BPo＋CPoと等しい。
したがって、図２から、N＝A、L＝B、M＝Cとなるのは、 AP＋BP＋CP≧APo＋BPo＋CPoである。（証明終）

　以上の証明から、内角120°の限界である正六角形と、１つの内角が120°を超える三角形の頂点でも、石けん膜の実験をしてみた。
　その結果、正六角形の場合は、内側にフェルマー点が６つでき、雪の結晶のような正六角形となった。できた正六角形の大きさはいつも同じとは限らない。１内角が120°以上の三角形では、フェルマー点はできなかった。

〈３〉石けん膜を使い、地図上での 最短経路を見つけ出す

（１）クラスメート39人を家庭訪問するとして、A～Eの５地区に分け、平行板に地図を重ねて家の場所に釘をさし、学校からの経路を探す。

《結果》

見つけた経路はA地区（学校を含めて９カ所）：３通り（フェルマー点各３つ）、B地区（９カ所）：３通り（同１、３つ）、C地区（９カ所）：２通り（同各３つ）、D地区（８カ所）：３通り（同２、３つ）、E地区（９カ所）：２通り（同各２つ）。
　（２）日本全国の県庁所在地（47カ所）を通る経路。石けん膜では４通り（フェルマー点は５、６、９つ）見つかった。

〈４〉石けん膜を用いなくても、 経路が分かる方法

　石けん膜ではフェルマー点と各地点を結ぶ線分で最短経路が示されることが分かった。そこで、フェルマー点を表す120°に分かれた３本の棒（「フェルマー定規」と称す）と線分を表す棒（「線分定規」と称す）を作った。地図上で試したら、うまく最短経路を導き出すことができた。

感想

　平行板を作るのが大変だった。県庁所在地の間が狭く、最短経路が分からなくなることがあった。フェルマー点の重要性も分かった。自然界では、ハチの巣が120°の集合体である正六角形でできていたり、ハチが最短で花と花を行き来するとも言われる。ハチに120°の概念が根付いているのではないか。