秋山仁特別賞
お父さんの薬がみつからないっ!
![]()
佐藤 華純
- 秋田県由利本荘市立本荘東中学校 3年
佐藤 華純 -
第47回入賞作品
中学校の部
秋山仁特別賞
父はたくさんの薬を飲んでいる。母の手製の箱に、薬のパッケージを細長く切って入れているが、目当ての薬がなかなか見つからない。下を向いていることが多いのだ。どうして下向きになるのか。上向きにしておく方法はないのだろうか。これらを解決するために、研究することにした。
| ① | 本当に薬のパッケージが下向きになっていることが多いのか確かめる。 |
| ② | 下向きになる理由を明らかにする。 |
| ③ | きちんと上向きにしておく方法を見つける。 |
(1)本当に下向きになっていることが多いのか。
細長く切ったパッケージにサインペンで印を付け、父がすべての薬を飲んで就寝する夜11時に、1カ月間毎日調べた。その結果、上向きになっていたのは8日、下向きが22日、横向きで箱の壁に張り付いていたのが1日あった。確かに「下向き」が多い。
(2)どうして「下向き」が多いのか。
1:準備したこと
 (i)実験装置「こまわり君」の開発と利用
(i)実験装置「こまわり君」の開発と利用
上面か下面かで、実験者の意図が表れてはいけないので実験装置を作成。箱を回転(5回転と設定)させることで最終的にどちらの面が上になるか確かめる。
(ii)カイ2乗検定
回転実験は100回繰り返す。上向きになった回数、下向きになった回数に違いがあるのか、ないのかを検定するために「カイ2乗検定」を用いる。この検定法は、データから期待値を算出し、それと実際の値がどれくらいずれているかで、偶然に起こり得る可能性を求める方法だ。棄却値はα = 5 % に設定、パソコン(Excel)で計算した。
2:薬のパッケージ1個の場合
《仮説1》薬のパッケージは、元々下向きになりやすい。
→薬は板状の部分にぶら下がっているように見えるので、下向きの方が安定するのではと考えたが、上面も下面も同じような割合だった。
3:1列につながったパッケージの場合
《仮説2》1列につながることで下向きになりやすい。
→薬が何個かつながることで下向きの力が大きくなり、安定度が増すのではないか。2~7個つながったパッケージで実験した。結果は薬のつながる数と上向き、下向きになる回数の間には、とくに関係はない。最も大きな差のあった6個のつながりの時についてカイ2乗検定を行った。 カイ2乗=1.29<3.84(α=5%)により、「帰無仮説」は棄却されない。すなわちこれは「偶然に起こり得ること」だった。
4:他の薬と混ぜた場合
《仮説3》箱の中で薬のパッケージどうしがぶつかり合い、からみあう中で下向きになっていくのではないか。
→「下向き」がわずかに多かったが、カイ2乗検定では「偶然に起こり得ること」だった。
5:反ったパッケージの場合
もう一度、箱の中を観察してみた。細長く切ったパッケージには反っているものが多いという特徴を発見した。
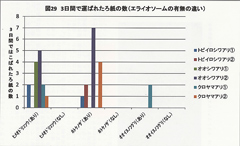
《仮説4》パッケージが反ることによって、下向きになりやすくなるのではないか。 →「下向き」(73%)が「上向き」(27%)より多かった。カイ2乗=11.2>3.84(α=5%)により、 「帰無仮説」は棄却される。すなわちこれは「偶然に起こり得ないこと」だった。
(3)反ったパッケージの条件を変えると、向きのなりやすさはどう変化するか。
1:「反り」の大きさを変えた場合
薬のパッケージは柔らかく、簡単に「反り」の大きさが変わってしまうのでアルミ板(100mm×17mm、厚さ0.8mm、質量3.5g)を使った。「反り」は正円の弧を描くように作り、「反り率」で表した。
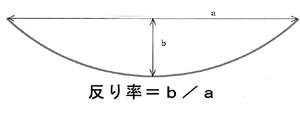
《予想》反り率が大きくなると、弧の外面が下になった方が安定するので、「下向き」が増えるのではないか。
→反り率が大きくなるにしたがい「上向き」が減少し、新たに「横向き」も増加する。「横向き」を 除外しカイ2乗検定をすると、確かに予想通りとなった。
2:長さを変えた場合
アルミ板の反り率0.1、長さ2cm 、4cm、6cm、8cm、10cmで調べる。
《予想》長さが短くなるにしたがい、「下向き」になりにくくなるのではないか。 →長さが短くなると上向きになる回数が増え、「横向き」も減る。4cm以下では「横向き」はなくなる。
3:幅を変えた場合
これまでの経験では、幅の広いパッケージは下向きになっていることが少ない。アルミ板の反り率0.1、幅17mm、34mm、51mm、68mm、85mmで調べた。
《予想》幅が大きくなるほど、「上向き」が多くなるのではないか。 →幅が大きくなると上向きの回数が増え、幅68mm以上になると、上向き・下向きの差は意味を もたないほど小さくなる。
(4)反ることによって、どうして下向きになりやすくなるのか。
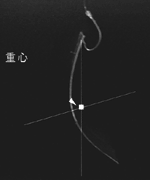
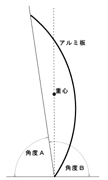
重心にヒントがあると考え、反ったアルミ板の重心を「つり下げ法」によって調べた。
→反ったパッケージが下向きになりやすいのは、重心の位置が弧の内側にあり、弧の外面の方向に倒れる範囲(角度)が広くなるためだ。
(5)重心の位置から①反りの大きな物体②長い物体③幅の小さい物体――が下向きになりやすい。
(6)どうして薬のパッケージは反るのか。
| ① | 温度変化説:ホットプレートで温めたり、冷蔵庫で冷やしたが反らなかった。 |  |
| ② | 湿度変化説:湯気の中に浸したり、ドライヤーの温風で乾燥させたりしたが反らなかった。 | |
| ③ | 外部圧力説:はさみで切る時に、下向きの力がはたらくために反った。反り方は紙を切った時よりも大きく、自然には元に戻らない。パッケージはプラスティック板とアルミはくの2層構造となっている。変形しやすいアルミはくが大きく曲がる |
(7)箱の中の薬のパッケージが、下向きにならないようにする方法はないか。
| ① | 逆反らし法:パッケージを逆に反らして入れる。 |
| ② | クリップ法:細く切ったパッケージの一方の端をクリップではさみ、下向きへの回転を防ぐ。 |
| ③ | 2つ折り法:パッケージを2つに折り、裏も表もない状態にする。 |
| ④ | 2つ折りクリップ法:パッケージを2つ折りにした上で、開かないように一方の端をクリップで止める。 |
→父の協力で1週間ずつ試したところが有効で、クリップが色付きだともっと見分けやすい。
(8)生活の中の「反り」(イナバウアー効果)を探してみる。
| ① | フォークやスプーン:フォークで実験したところ反りの外面(背中側)が下になることが多い。床などに落としてもこの姿勢になることが多いということだ。 |
| ② | 電話の受話器:スピーカーやマイクは、反っていることによって、床にぶつかるようなことが少なくなる。 |
| ③ | 人間:背中が外、腹が内となるように曲がっているため、大切な内臓が守られている。 |
今後の課題
| ① | 上向き・下向きの出方(実験結果)と計算で予想される出方(理論値)を一致させることができないか検証したい。 |
| ② | 生活の中の「反り」をもっとたくさん見つけ、役割を科学的に検証したい。 |
| ③ | 根本的に父は薬の飲みすぎだ。薬を飲まずに、健康でいられるような生活をすべきだ。 |
審査評[審査員] 秋山 仁
格子状に錠剤の入ったパッケージに関する研究である。何種類かの薬のパッケージを帯状に切って、薬箱にしまっておくと、薬の入った面が下を向いてしまい、目当ての薬を見つけにくいことが往々にしてあるという事実に端を発し、その謎解きが始まった。すなわち、研究の目的は次の3点の解明である。
| ① | 薬のパッケ一ジは下向きになる傾向があるのか? |
| ② | もし、そうならばその理由は何か? |
| ③ | そうならない具体策を見付ける |






















指導について由利本荘市立本荘東中学校 佐藤和広
この研究の指導にあたって、1つ悩んだことがあった。それは、「カイ2乗検定」を教えるべきかどうかということである。統計学は中学校では学習しない。中学生のレベルを超えたものを指導してよいのかということについて迷いが生じた。
そんなとき、世界の理科研究について述べたある大学教授の文章を目にした。日本では「子どもらしさ」を求める指導者が多いが、欧米や日本以外のアジア諸国では「子どもでも限界を定めない」ということが述べられていた。この指導者の姿勢が、各国の研究レベルに影響しているそうである。
これを見て私は「カイ2乗検定」を指導することを決心した。実際に指導してみると、意外と簡単に理解させることができた。子どもの頭は想像以上に柔らかい。その吸収力に大人は全くかなわない。科学研究において「子どもには無理」という偏見は捨てなければいけないことを実感した。